Синхронизируемые автоматы
Последнее изменение: 09/09/2021 18:41:35В семестровом спецкурсе будет обсуждён ряд актуальных задач теории конечных автоматов, в частности, гипотеза Черни о синхронизируемых автоматах и ее обобщения, а также задача о раскраске дорог.
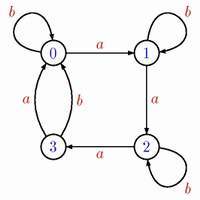
На рисунке представлен синхронизируемый автомат: можно проверить, что слово baaabaaab синхронизирует его, т.е. переводит в состояние, не зависящее от того, в каком состоянии автомат находился первоначально. Гипотеза Черни утверждает, что для любого синхронизируемого автомата с n состояниями существует синхронизирующее слово длины (n-1)^2. (В примере на рисунке n=4 и указанное слово имеет длину 9=(n-1)^2.) Вопрос о её справедливости остаётся открытым уже более 50 лет.
В спецкурсе будет освещено современное состояние теории синхронизируемых автоматов и предложено несколько задач для исследовательской работы.
Для понимания спецкурса требуется владение базовым курсом линейной алгебры (2-й семестр 1-го курса) и элементами теории графов. Желательно (но необязательно) представление об NP-полных задачах. Предварительные знания по теории автоматов не предполагаются. Отчётность - экзамен или зачет (по выбору слушателя). Формально спецкурс адресован студентам потока ФИИТ (3-й -4-й курсы), но приглашаются все заинтересованные студенты бакалавриата и магистратуры.
Спецкурс читается по понедельникам 2-й парой в MS Teams.
Литература: М.В.Волков, Синхронизация конечных автоматов. I
Лекция 1: определение, история, мотивация
Мы вводим понятие синхронизируемости для классического случая полных детерминированных автоматов. Объяснив, что такое синхронизируемость, мы также обсуждаем, где и когда возникало это понятие, - оно часто переоткрывалось математиками, информатиками и инженерами.
Слайды лекции (на английском языке)
Лекция 2: Алгоритмические аспекты
Излагаются алгоритм Лю-Черни проверки автомата на синхронизируемость и жадный алгоритм построения синхронизирующего слова.
Слайды лекции (на английском языке) + Версия для печати
Лекция 3: Теоретико-сложностные аспекты
Обсуждается сложность ряда естественных задач, возникающих при синхронизации конечных автоматов: задачи существования синхронизирующего слова данной длины, задачи нахождения длины кратчайшего синхронизирующего слова, задачи существования синхронизирующего слова предписанного вида.
Слайды лекции (на английском языке) + Версия для печати
Лекция 4: Гипотеза Черни
Доказывается нижняя оценка (n-1)^2 на максимум порогов синхронизируемых автоматов с n состояниями. Формулируется и обсуждается гипотеза Черни о точности этой нижней оценки.
Слайды лекции (на английском языке) + Версия для печати
Лекция 5: Метод расширения
Обсуждается метод расширения. Доказывается верхняя оценка n^2-3n+3 на порог синхронизации эйлеровых синхронизируемых автоматов с n состояниями
Слайды лекции (на английском языке) + Версия для печати
Лекция 6: Автоматы с нулем
Доказывается верхняя оценка n(n-1)/2 на порог синхронизации синхронизируемых автоматов с n состояниями, одно из которых является нулем автомата, и точность этой оценки для автоматов с нулем над неограниченным алфавитом. Обозреваются недавние результаты о пороге синхронизации синхронизируемых автоматов с нулем и двумя входными буквами.
Слайды лекции (на английском языке) + Версия для печати
Лекция 7: Апериодические автоматы
Доказывается верхняя оценка n(n-1)/2 на порог синхронизации апериодических синхронизируемых автоматов с n состояниями.
Слайды лекции (на английском языке) + Версия для печати