Волков Михаил Владимирович: Темы курсовых работ

Последнее изменение: 26/12/2024 18:24:24

Темы курсовых работ для студентов 3-4 курсов

Проблема конечного базиса тождеств для полугрупп унитарных подмножеств в группе

Подмножество группы назовем унитарным, если оно содержит единицу группы. Совокупность U(G) всех унитарных подмножеств данной группы G образует полугруппу относительно операции умножения подмножеств. При каких условиях на конечную группу G полугруппа U(G) имеет конечный базис тождеств? Аналогичный вопрос представляет интерес для подполугруппы в U(G), порожденной подгруппами группы G.

Проблема конечного базиса тождеств для полугрупп дважды стохастических матриц

Квадратная матрица с неотрицательными действительными элементами называется дважды стохастической, если сумма элементов в каждой ее строке и в каждом ее столбце равна 1. Нетрудно понять, что множество DS_n всех дважды стохастических матриц nxn-матриц замкнуто относительно умножения и транспонирования матриц, т.е. образует инволютивную полугруппу. Задача состоит в исследовании тождеств DS_n как полугруппы и как инволютивной полугруппы.

Нижние оценки порога синхронизации для сильно связных апериодических автоматов

Конечный автомат называется

  • апериодическим, если моноид его переходов не содержит нетривиальных подгрупп;
  • сильно связным, если его граф сильно связен;
  • синхронизируемым, если существует слово w такое, что любой путь в автомате, вдоль которого читается w, заканчивается в одном и том же состоянии (такое слово w называется синхронизирующим).

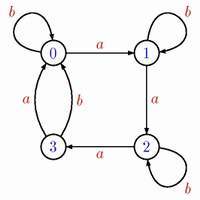Image:cerny4.jpg На рисунке изображен сильно связный синхронизируемый (но не апериодический!) автомат. Кратчайшее синхронизирующее слово для него - baaabaaab.

Известно (см. [1]), что сильно связный апериодический автомат синхронизируем и, если в таком автомате n состояний, то у него есть синхронизирующее слово длины не больше [n(n+1)/6]. В то же время никакие нетривиальные нижние оценки для порога синхронизации, т.е. длины кратчайшего синхронизирующего слова, для сильно связных апериодических автоматов с n состояниями пока неизвестны. Задача состоит в том, чтобы либо найти такие нижние оценки, либо улучшить указанную верхнюю оценку из [1].

Литература:

  1. M.V.Volkov, Synchronizing automata preserving a chain of partial orders, Theor. Comput. Sci. 410 (2009), 3513-3519.

Синхронизация автоматов как игровая задача

Определение синхронизируемого автомата см. выше. На процесс синхронизации можно смотреть как на игру по следующим правилам. Игровым полем является граф автомата. В начальный момент каждое состояние автомата покрыто фишкой. Каждая буква из входного алфавита автомата задает ход: все фишки скользят вдоль стрелок, помеченных данной буквой и оказываются на новых состояниях. При этом если на каком-то состоянии после хода оказывается более одной фишки, то все фишки, кроме одной, снимаются.

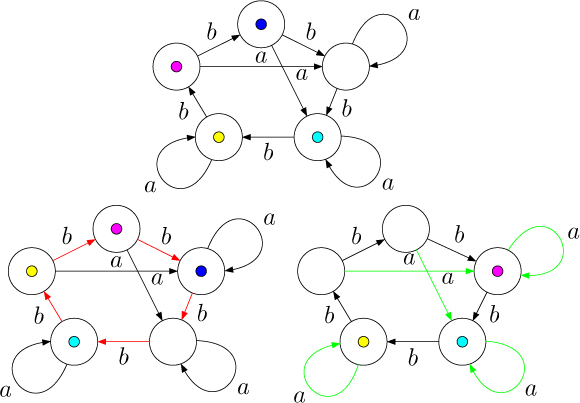Image:synchrogame.jpg На рисунке сверху показано некоторое расположение фишек на одном автомате с пятью состояниями и входным алфавитом {a,b}. Внизу слева показано, как изменится расположение фишек, если сделать ход, соответствующий букве b, а справа показан результат хода, отвечающего букве a.

Игра считается выигранной, если после некоторой последовательности ходов на игровом поле останется ровно одна фишка. Нетрудно сообразить, что выиграть в описанной игре можно в том и только том случае, когда автомат синхронизируемый, а выигрывающие последовательности ходов в точности соответствуют синхронизирующим словам.

Теперь предположим, что в игру по описанным правилам играют два игрока: Алиса и Боб. Они ходят поочередно, причем первой ходит Алиса. Ее цель - как можно быстрей синхронизировать автомат, т.е. придти к позиции, когда на игровом поле останется ровно одна фишка. Цель Боба прямо противоположная - воспрепятствовать синхронизации. Будем считать, что Боб побеждает, если на игровом поле повторится позиция, в которой присутствует больше одной фишки. Такую игру будем назвать игрой синхронизации на данном автомате.

Ряд естественных задач об играх синхронизации разобран в [1]. Предлагается исследовать такие вопросы:

  1. Как долго может продолжаться игра? Существует ли такая серия автоматов с неограниченно растущим числом состояний, что в игре синхронизации на каждом автомате из этой серии может быть сделано не ограниченное никаким полиномом от числа состояний число ходов?
  2. Какова вычислительная сложность задачи, входными данными которой служат автомат А и натуральное число К и требуется узнать, сможет ли Боб победить в игре синхронизации на А, сделав не более К ходов? (Аналогичная задача для Алисы решена в [1].)

Предлагается также исследовать модификацию игры синхронизации, в которой очередность ходов Алисы и Боба определяется некоторым потенциально бесконечным вправо направляющим словом w над алфавитом {a,b}: слово w побуквенно читают слева направо, и Алиса ходит всякий раз, когда прочитана буква а, а Боб - всякий раз, когда прочитана буква b. ("Стандартная" игра синхронизации, описанная выше, соответствует направляющему слову ababab....)

Литература:

  1. F. M. Fominykh, P. V. Martyugin, M. V. Volkov. P(l)aying for synchronization, Int. J. Foundations Comp. Sci. 24, no. 6 (2013), 765-780.

Нижние оценки порога синхронизации для нетотально синхронизируемых автоматов

Перекраской автомата А называется любой автомат А', полученный из А некоторой последовательностью перестановок букв на стрелках, исходящих из каждого состояния. Автомат называется тотально синхронизируемым, если все его перекраски - синхронизируемые автоматы. Например, можно проверить, что автомат, изображенный на рисунке выше, тотально синхронизируемый.

Как и выше, будем называть автомат с n состояними n-автоматом. Все известные на сегодня (см. [1]) медленно синхронизируемые автоматы, т.е. n-автоматы с порогом синхронизации, близким к (n-1)^2, тотально синхронизируемы. Наилучшая нижняя оценка для порога синхронизации нетотально синхронизируемых n-автоматов, которую можно извлечь из известных примеров, имеет порядок n^2/2. Интересно было бы улучшить эту оценку, указав серию примеров нетотально синхронизируемых n-автоматов с порогом синхронизации, более близким к (n-1)^2.

Литература:

  1. Д.С.Ананичев, М.В.Волков, В.В.Гусев. Примитивные орграфы с большими экспонентами и медленно синхронизируемые автоматы, Записки научных семинаров ПОМИ. (Комбинаторика и теория графов. IV) 402 (2012), 9-39.

Расстояние редактирования до синхронизированного автомата

Известно, что если граф автомата А сильно связный и наибольший общий делитель длин его циклов равен 1, то существует перекраска автомата А, которая является синхронизируемым автоматом. (Это так называемая теорема о раскраске дорог, она доказана в 2007-м году.) Переключением назовем обмен меток двух рёбер, исходящих из некоторой вершины. Таким образом, перекраска - это некоторая последовательность переключений. Допустим, что дан автомат с сильно связным графом и наибольшим общим делителем длин циклов, равным 1, и мы хотим перекрасить его в синхронизируемый автомат. Сколько переключений может для этого понадобиться? Интерес представляет максимум числа необходимых переключений, а так же то, на каких автоматах этот максимум достигается.

Понятно, что искомый максимум зависит от числа состояний и числа букв автомата. Можно для начала ограничиться случаем автомата с двумя буквами.

Деревья минимального веса

Рассматриваются полные бинарные деревья, т.е. деревья, в которых каждый узел, не являющийся листом, имеет ровно двух сыновей. Весом листа такого дерева называется произведение числа правых и левых ребер в пути от корня дерева к этому листу; весом дерева называется сумма весов его листьев. 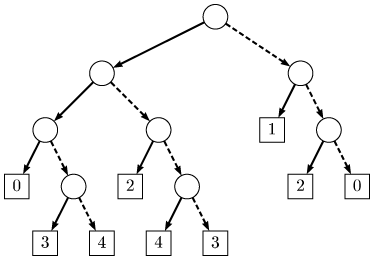Image:tree.png На рисунке изображено дерево веса 19; внутри каждого листа указан его вес.

Пусть у дерева n листьев. Каков минимальный вес такого дерева? Сколько существует деревьев минимального веса?

Задача имеет важные приложения в теории автоматов.

Сложность вычисления эффективной размерности

Пусть G=(V,E) - конечный ориентированный граф (возможно с петлями, но без кратных ребер). Матричной реализацией размерности n для графа G называется взаимно однозначное отображение F объединения множеств V и E во множество М, состоящее из |V|+|E| матриц размера nxn над полем комплексных чисел и такое, что произведение двух матриц Х и Y из М равно матрице Z из М в случае, когда X=F(v), Y=F(v'), Z=F(e), где v,v' - вершины, а е - ребро с началом v и концом v', и равно нулевой матрице во всех остальных случаях. Эффективной размерностью графа G называется наименьшая размерность его матричной реализации. Например, для графа с одной вершиной v и петлей e эффективная размерность равна 3, так как легко указать две такие 3х3-матрицы X=F(v) и Z=F(e), что XX=Z и XZ=ZX=ZZ=0, но 2х2-матриц с такими свойствами не существует. Известно, что задача вычисления эффективной размерности данного графа принадлежит классу PSPACE. Требуется доказать (или опровергнуть), что она является NP-трудной.

Темы курсовых работ для студентов 2-3 курсов

Сопровождение сайта кафедры (несколько тем)

  1. Прикрутить исправление ошибок с помощью системы Orphus
  2. Прикрутить RSS
  3. Спроектировать и создать базу публикаций кафедры и удобный интерфейс к ней
  4. Написать скрипты, которые собирали бы информацию о цитированиях работ сотрудников кафедры с сайтов MathSciNet, Web of Science, Google Scholar и т.п.

Смотрите также: