Алгебра и геометрия
Последнее изменение: 18/02/2021 13:03:18Основной курс для потока ФИ/ПИ первого курса. В осеннем семестре 2014/15 учебного года читался по понедельникам с 14:30 в ауд. 611, а по четным неделям - еще и по четвергам с 12:50 в ауд. 622.
Экзамен проходил в ауд. 605 с 9:00:
- для группы ФИ-101 во вторник, 20.01.2015;
- для группы ПИ-101 в среду, 21.01.2015.
| Группа | Отлично | Хорошо | Удовлетв. | Неудовл. | Не аттест. | Всего |
|---|---|---|---|---|---|---|
| ФИ-101 | 12 | 4 | 6 | 6 | 2 | 30 |
| ПИ-101 | 4 | 6 | 7 | 5 | 22 | |
| Поток | 12 | 8 | 12 | 13 | 7 | 52 |
| Группа | Отлично | Хорошо | Удовлетв. | Неудовл. | Не аттест. | Всего |
|---|---|---|---|---|---|---|
| ФИ-101 | 4 | 2 | 2 | 8 | ||
| ПИ-101 | 5 | 1 | 6 | 12 | ||
| Поток | 9 | 3 | 8 | 20 |
Краткое содержание курса
- Матрицы и определители
- Действия над матрицами - сложение, транспонирование, умножение. Свойства действий.
- Определитель квадратной матрицы; основные теоремы об определителях - теорема единственности, теорема существования, теорема симметрии. Определитель Вандермонда. Определитель полураспавшейся матрицы. Определитель произведения матриц. Явное выражение определителя через элементы матрицы.
- Обратная матрица; правило Крамера для решения систем линейных уравнений. Практический алгоритм вычисления обратной матрицы.
- Комплексные числа
- Формула Кардано
- Понятие поля; построение поля комплексных чисел
- Действия с комплексными числами
- Корни из единицы и их приложения
- Линейная алгебра и геометрия
- Линейные пространства. Базис, размерность.
- Координаты вектора. Замена координат
- Векторная алгебра трехмерного пространства
- Уравнения прямой и плоскости в трехмерном пространстве
- Основные метрические задачи на прямую и плоскость
- Квадрики на плоскости и в пространстве
- Эллипс, гипербола, парабола
- Упрощение уравнения 2-го порядка от двух переменных. Классификация плоских квадрик
- Эллипсоиды, гиперболоиды, параболоиды, конусы, цилиндры
Вопросы к экзамену
- Матрицы и действия над ними. Свойства действий над матрицами.
- Аксиомы определителя и их следствия.
- Теорема единственности определителя.
- Теорема существования определителя.
- Теорема симметрии.
- Определитель полураспавшейся матрицы.
- Определитель произведения двух матриц.
- Определитель Вандермонда. Приложение к вычислению циркулянтов.
- Обратная матрица и ее нахождение.
- Приложение обратной матрицы к решению систем линейных уравнений. Формулы Крамера.
- Алгоритм вычисления обратной матрицы и его обоснование.
- Выражение определителя через его элементы.
- Формула Кардано.
- Конструкция поля комплексных чисел.
- Сопряженные комплексные числа. Модуль и аргумент комплексного числа. Тригонометрическая форма записи комплексного числа. Умножение и деление комплексных чисел в тригонометрической форме.
- Формула Муавра. Извлечение корня из комплексного числа.
- Корни из единицы и их свойства. Приложение к вычислению циркулянтов.
- Аксиомы линейного пространства. Линейная зависимость. Лемма о правом крайнем. Геометрический смысл линейной зависимости в трехмерном пространстве.
- Системы образующих и базисы. Теорема о существовании базиса.
- Теорема о равномощности базисов. Размерность пространства. Теорема о продолжении.
- Координаты вектора. Связь координат в разных базисах. Критерий равенства определителя нулю.
- Скалярное произведение в трехмерном пространстве. Свойства скалярного произведения. Скалярное произведение в координатах.
- Векторное и смешанное произведения в трехмерном пространстве. Теорема о смешанном произведении.
- Свойства векторного произведения. Векторное и смешанное произведения в координатах.
- Основная теорема об уравнении прямой на плоскости.
- Основная теорема об уравнении плоскости.
- Прямая в пространстве. Взаимное расположение прямой и плоскости. Взаимное расположение двух прямых.
- Основные метрические задачи на прямую и плоскость.
- Эллипс. Вывод канонического уравнения, директориальное свойство.
- Гипербола. Вывод канонического уравнения, директориальное свойство.
- Парабола. Вывод канонического уравнения.
- Преобразование координат на плоскости. Формулы преобразования координат при переносе начала координат и при повороте.
- Упрощение уравнения 2-го порядка от двух переменных. Случай центральной квадрики.
- Упрощение уравнения 2-го порядка от двух переменных. Случай нецентральной квадрики.
- Эллипсоиды, гиперболоиды, параболоиды. Исследование их формы с помощью метода сечений.
Контрольные вопросы по прочитанным лекциям
- Действия над матрицами
- Показать, что для каждой матрицы А существует такая матрица В, что А+В=0. (Такая матрица называется противоположной матрице А.)
- Привести пример двух ненулевых матриц, произведение которых равно нулю.
- Следом квадратной матрицы называется сумма элементов, стоящих на ее главной диагонали. Проверить, что если А и В - квадратные матрицы одинакового размера, то след АВ равен следу ВА. Верен ли аналогичный результат, если А и В - такие прямоугольные матрицы, что оба произведения АВ и ВА существуют?
- Квадратная матрица называется симметрической, если она совпадает со своей транспонированной. Доказать, что произведение любой матрицы (не обязательно квадратной) на ее транспонированную есть симметрическая матрица.
- Квадратная матрица называется кососимметрической, если она противоположна своей транспонированной. Доказать, что любую квадратную матрицу можно представить в виде суммы некоторой симметрической матрицы и некоторой кососимметрической матрицы, причем единственным образом.
- Квадратные матрицы А и В одинакового размера называются перестановочными, если АВ=ВА. Доказать, что произведение двух симметрических матриц будет симметрической матрицей тогда и только тогда, когда эти матрицы перестановочны. (Этот простой факт имеет принципиальное значение для квантовой механики.)
- Доказать, что квадратная матрица, перестановочная со всеми диагональными матрицами, сама является диагональной, а квадратная матрица, перестановочная со всеми матрицами, является скалярной, т.е. диагональной матрицей, у которой все элементы главной диагонали одинаковы.
- Определители
- Алиса и Боб по очереди заполняют числами матрицу 2х2. Алиса (которая ходит первой) хочет добиться, чтобы определитель получившейся матрицы был отличен от 0, а Боб хочет добиться, чтобы этот определитель был равен 0. У кого из игроков есть выигрышная стратегия? А если Алиса хочет, чтобы получился нулевой определитель, а Боб - чтобы получился определитель, отличный от 0? Те же вопросы для матрицы 3х3. (Предостережение: для 3х3-матриц задача уже нетривиальна.)
- Пусть определитель nxn-матрицы A равен d. Чему равен определитель матрицы kА?
- nxn-матрица называется матрицей Адамара, если произведение этой матрицы на ее транспонированную равно nE. (На лекции были приведены конкретные примеры матриц Адамара для случая, когда n есть степень двойки.) Чему равен определитель матрицы Адамара?
- (Теорема Гамильтона-Кэли) Пусть А - 2х2-матрица, s - ее след, а d - ее определитель. Проверить, что А^2-sA+dE=0.
- Через tr(A) обозначается след матрицы А. Доказать, что удвоенный определитель 2х2-матрицы А равен tr(A)^2-tr(A^2).
- Привести пример 4х4-матрицы, определитель которой не равен ad-bc, где a - определитель верхнего левого 2х2-блока, b - определитель верхнего правого 2х2-блока, c - определитель нижнего левого 2х2-блока, d - определитель нижнего правого 2х2-блока.
- Доказать, что для любой 3х3-матрицы среди 6 слагаемых в явном выражении определителя этой матрицы через ее элементы обязательно найдутся числа разных знаков.
- Доказать, что определитель кососимметрической матрицы нечетного порядка равен 0.
- Пусть в nxn-матрице А есть такие s строк и t столбцов, что все элементы, стоящие на их пересечении, равны 0 и s+t>n. Доказать, что определитель матрицы А равен 0.
- (Формула Бине-Коши) Пусть А есть nxk-матрица, а В - kxn-матрица. Тогда произведение АВ есть nxn-матрица. Доказать, что определитель матрицы AB равен нулю, если k<n, и равен сумме попарных произведений соответствующих друг другу миноров порядка n, если k>n. (Cумма берется по всем наборам столбцов матрицы A и строк матрицы B с возрастающими номерами i_1<i_2<...<i_n; миноры матриц A и B порядка n называются соответствующими друг другу, если они стоят в столбцах матрицы A и строках матрицы B с одинаковыми номерами.)
- (Теорема Лапласа) Пусть М - минор квадратной матрицы А. Его алгебраическим дополнением называется определитель подматрицы, полученной вычеркиванием строк и столбцов, в которых стоит М, если сумма номеров этих строк и столбцов четна, и тот же определитель, взятый со знаком "минус", если эта сумма нечетна. Доказать, что для любого набора строк матрицы А ее определитель равен сумме произведений всех миноров, заключенных в данных строках, на их алгебраические дополнения.
- Обратная матрица
- Пусть А - обратимая матрица. Доказать, что транспонированная матрица А^t обратима и матрица, обратная к А^t, получается транспонированием из матрицы, обратной к А.
- Пусть А и В - обратимые матрицы. Доказать, что матрица АВ обратима и матрица, обратная к АВ, равна произведению матрицы, обратной к В, на матрицу, обратную к А.
- Доказать, что матрица, обратная к верхнетреугольной матрице, сама является верхнетреугольной.
- Пусть определитель матрицы А равен d. Найти определитель присоединенной к А матрицы.
- Доказать, что при перестановке двух строк матрицы в присоединенной матрице происходит такая же перестановка столбцов и все элементы присоединенной матрицы меняют знак.
- Доказать, что матрица, присоединенная к АВ, равна произведению матрицы, присоединенной к В, на матрицу, присоединенную к А. (Указание - сначала докажите это свойство для невырожденных матриц, а потом представьте произвольную матрицу в виде предела невырожденных и воспользуйтесь тем, что определитель есть непрерывная функция элементов матрицы.)
- Комплексные числа
- Доказать, что коммутативность сложения можно вывести из остальных аксиом поля. (Предостережение: задача весьма нетривиальна.)
- Доказать, что модуль суммы двух комплексных чисел не превосходит суммы их модулей.
- Квадратная матрица над полем комплексных чисел называется эрмитовой, если каждый ее элемент сопряжен с элементом, симметричным ему относительно главной диагонали. Доказать, что определитель эрмитовой матрицы - действительное число.
- Найти сумму k-х степеней всей корней n-й степени из 1.
- Найти произведение всех корней n-й степени из 1.
- Линейные пространства
- Доказать, что коммутативность сложения можно вывести из остальных аксиом линейного пространства. (Предостережение: задача нетривиальна.)
- Доказать, что базис пространства можно определить как максимальную линейно независимую систему или как минимальную систему образующих.
- Вычислить размерность пространства всех симметрических nxn-матриц.
- Пусть в пространстве имеются три базиса, Т - матрица перехода от 1-го базиса ко 2-му, а S - матрица перехода от 2-го базиса к 3-му. Найти матрицу перехода от 1-го базиса к 3-му.
- Векторная алгебра трехмерного пространства
- Матрица Грама базиса е_1,е_2,е_3 - это 3х3-матрица, у которой на месте (i,j) стоит скалярное произведение e_ie_j. Доказать, что определитель матрицы Грама отличен от 0.
- Как связаны между собой матрицы Грама двух разных базисов?
- Доказать тождество Якоби [[a,b],c]+[[b,c],a]+[[c,a],b]=0.
- Пусть е_1,е_2,е_3 - базис. Доказать, что вектора [е_1,е_2], [е_3,е_1], [е_2,е_3] также образуют базис. (Указание - эту задачу можно решать разными способами, но довольно поучительно перейти к координатам.)
- Уравнения прямой и плоскости в трехмерном пространстве
- Исследовать взаимное расположение трех прямых на плоскости. (Здесь и далее под словом "исследовать" понимается следующее: указать условия на коэффициенты уравнений, отвечающие различным с геометрической точки зрения вариантам взаимного расположения задаваемых этими уравнениями объектов).
- Исследовать взаимное расположение трех плоскостей в пространстве.
- На плоскости даны три параллельные прямые с уравнениями Ax+By+C=0, Ax+By+D=0, Ax+By+E=0. Указать необходимое и достаточное условие, при котором вторая прямая проходит между первой и третьей.
- В пространстве даны три параллельные плоскости с уравнениями Ax+By+Cz+D=0, Ax+By+Cz+E=0, Ax+By+Cz+F=0. Указать необходимое и достаточное условие, при котором вторая плоскость проходит между первой и третьей.
- В пространстве даны две параллельные плоскости с уравнениями Ax+By+Cz+D=0, Ax+By+Cz+E=0 и прямая с уравнением x=x_0+mt,y=y_0+nt, z=z_0+pt. Указать необходимое и достаточное условие, при котором прямая расположена между плоскостями.
- Эллипс, гипербола, парабола
- Доказать, что площадь эллипса с полуосями a и b больше чем 2ab, но меньше чем 4ab. (На самом деле эта площадь равна πab, но доказать это элементарными средствами сложно.)
- Доказать, что у параболы нет асимптот.
- Доказать, что произведение расстояний от любой точки гиперболы до ее асимптот есть величина постоянная.
- Найти длину отрезков (считая от центра гиперболы), отсекаемых директрисами гиперболы от на ее асимптотах.
- Доказать, что директриса гиперболы проходит через проекции соответствующего ей фокуса на любую асимптоту.
- Найти расстояние от фокуса гиперболы до ее асимптоты.
- (Шары Данделена) Круговой конус рассечён плоскостью, не проходящей через центр конуса. В него вписаны две сферы, касающиеся поверхности конуса и секущей плоскости, как показано на рисунке
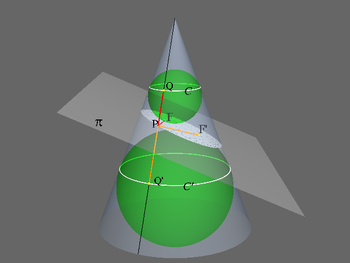 . Доказать, что точки F и F', в которых сферы касаются секущей плоскости, служат фокусами эллипса, получающегося в сечении.
. Доказать, что точки F и F', в которых сферы касаются секущей плоскости, служат фокусами эллипса, получающегося в сечении.
Литература для дополнительного чтения
- В. В. Прасолов. Задачи и теоремы линейной алгебры
- Алгоритм Штрассена
- Carl D. Meyer. Matrix Analysis and Applied Linear Algebra